Da ist mir doch tatsächlich beim Durchsehen uralter Sicherungskopien ein ebenso uralter Artikel in die Hände gefallen, einer, den ich vor Ewigkeiten – als es noch keine Blogs, sondern nur einfache Webseiten gab. „Wie weit ist eigentlich der Horizont entfernt?“ – mal verfasst habe.

Und da die Basis der Handlung des Artikels auf Kreta stattfindet, bringe ich es nicht übers Herz, diesen wertvollen Beitrag wieder mit den Sicherungskopien verstauben zu lassen.

Viel Spaß also bei diesem Relikt aus dem letzten Jahrtausend…

Ein Beitrag von Kafenio.eu

Vorgeschichte

Vor einiger Zeit, um genau zu sein am Sonntag, dem 5. 9. 1999 so gegen 15 Uhr Ortszeit, sind wir in Chania auf Kreta entlang der Hafenmauer spaziert. Es hatte wohl reichliche 35°C im Schatten, vielleicht auch noch deutlich mehr. Das hat uns aber nicht weiter gestört, da unser kretisches Lustwandeln fand ohnehin fast ausschließlich im Sonnenschein stattgefunden hat. Und was interessiert es uns in der Sonne schon, wie warm es im Schatten ist?

Während wir Fische im Wasser beobachtend dahin geschlendert sind, ist mir urplötzlich in den Sinn gekommen, daß die Griechen ja eigentlich einen sehr eng begrenzten Horizont haben: Zu einer Stadt, die internationalChania heißt, sagen sie Hania und schreiben gar Xania.

Dieser Gedankengang hat in mir sofort einen ununterdrückbaren Wissensdurst geweckt: Wie weit ist eigentlich mein Horizont entfernt?

 

Durch diese plötzlich hervorgerufenen Selbstzweifel völlig verunsichert steuerten wir daraufhin sofort ein sehr nettes Kafenio an.

Hier begannen wir Überlegungen anzustellen, wie eigentlich die Entfernung des Horizontes zu berechnen war. Nach nur einem entliehenen Kugelschreiber, einer entwendeten Serviette, zwei doppelten Ouzo und zwei verirrten theoretischen Überlegungen waren unsere trigonometrischen Forschungen so weit gediehen, daß wir mit einer grobe Überschlagsrechnung – wer quält sich bei einer solchen Hitze schon gerne mit Dezimalstellen oder gar exakten Quadratwurzeln – unseren Horizont bestimmen konnten.

Das Ergebnis war – nachträglich betrachtet – recht genau, aber dennoch äußerst niederschmetternd. Um einen einigermaßen akzeptablen Horizont zu erlangen, hätte man zumindest einen Berg erklimmen müssen. Was bei gut 35°C im Schatten natürlich ein Ding der Unmöglichkeit ist. Aus lauter Frust darüber mussten wir uns noch einen Ouzo genehmigen, um den Alltag nach dieser Selbsterkenntnis besser ertragen zu können.

Theorie zur Berechnung der Entfernung zum Horizont

 

 

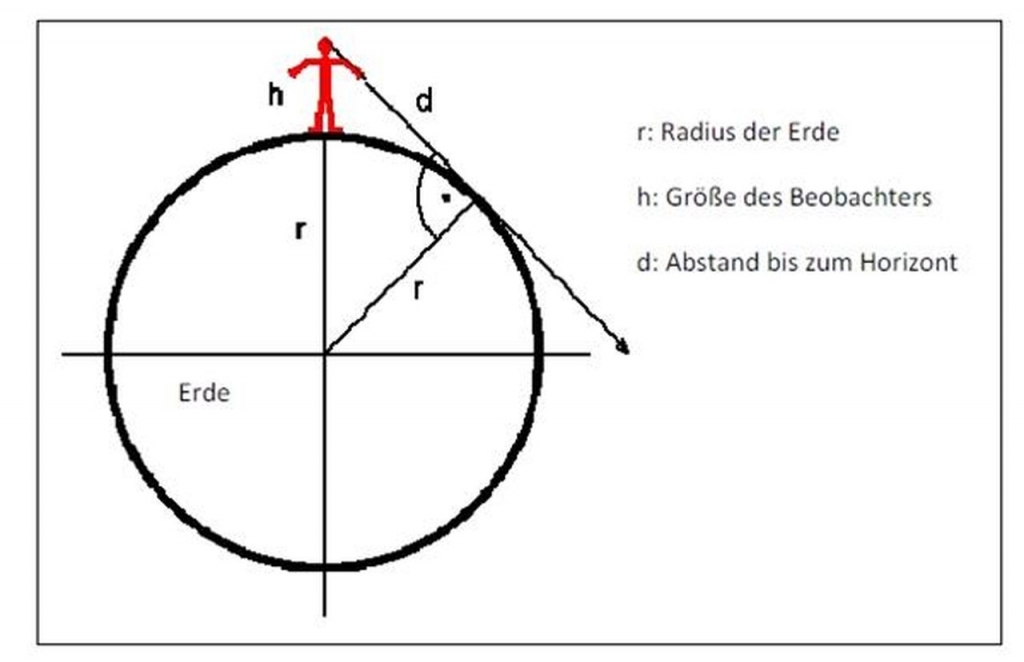
Wie aus dieser grenzgenialen Skizze (die Originalskizze ist leider auf der Serviette in besagtem Kafenio zurückgeblieben, aber es handelt sich hier um eine aus dem Gedächtnis rekonstruierten detailgetreuen Nachbildung) leicht zu erkennen ist, kann man mit Kenntnis der Werte der Platzhalter h und r und der Erkenntnis eines ziemlich alten aber auch ziemlich bekannten Griechens namens Pythagoras, sowie allgemein zugänglichem trigonometrischen Fachwissens die Unbekannte d berechnen.

Wissensbasis
r	Entfernung der Meereshöhe vom Erdmittelpunkt, gemeinhin als Erdradius bezeichnet.
h	Höhe der Augen des Horizontsuchenden über dem Meer.
d	Distanz des Horizontes vom Betrachter.
Eine beliebige Tangente eines Kreises steht immer normal zu der Strecke, die sich durch den Berührungspunkt des Kreises mit der Tangente und den Mittelpunkt des Kreises ergibt.
Die Summe der Quadrate der Katheten in einem rechtwinkeligen Dreieck ist gleich dem Quadrat der Hyptenuse.

Verbal ausgedrückt kann man also als obiger Skizze folgern, dass die Summe des Quadrates des Radius der Erde und des Quadrates der Distanz des Horizontes zum Auge des Horizontsuchenden gleich dem Quadrat des Abstandes der Augen des Horizontsuchenden vom Erdmittelpunkt ist. Wer diesen Satz bei 35%deg;C nach zwei Ouzo versteht sollte dringend einen Arzt aufsuchen.

Mathematisch-formal ausgedrückt heißt das:

r² + d² = ( r + h )²
Mittels einfacher Transformationen kann diese Formel in eine explizite Form bezüglich d gebracht werden.
r² + d² = r² + 2rh + h²
d² = 2rh + h²
d = ( 2rh + h² ) ^½ = sqrt( 2rh + h² )

Der Erdradius wird für die Äquatorregion mit 6378,388km, für die Polargebiete mit 6356,912km angegeben. Bei entsprechender Würdigung des Satzes der Impulserhaltung, des durchschnittlichen Kaloriengehaltes von 100ml Bier (45 bis 60kcal), des mittleren Abstandes des Planeten Jupiter zur Sonne und anderer hier völlig nutzloser theoretischer Konstrukte (zusammengefasst: empirischer erworbener Pragmatismus) entscheidet man sich am besten dafür, einfach das arithmetische Mittel zu bilden. Dadurch erhält man sicher einen brauchbaren Wert für unsere europäischen Breitengrade.

Für unsere Rechnung ergibt sich somit:

r = ½ ( 6356,912km + 6378,388km ) = 6367,65km

Das Problem der Augenhöhe ist im Allgemeinen leider nur empirisch zu ermitteln, ein Maßband leistet bei der Bewältigung dieser Aufgabe gute Dienste. Ist die Höhe der Augen aber erst einmal bekannt, steht einer Berechnung des eigenen Horizontes also nichts mehr im Wege.

Unten im Artikel findet sich ein einfacher Rechner, der es jedem erlaubt, seinen eigenen Horizont – oder den von beliebigen Mitmenschen – zu bestimmen.

Aus diesen Berechnungen ergeben sich doch einige wichtige Erkenntnisse.

• Da die Griechen eine geringere durchschnittliche Körpergröße als Mitteleuropäer haben, ist ihr Horizont tatsächlich etwas eingeengter als unserer. Man darf ihnen also ihre komische Sprech- und Schreibweise nicht übel nehmen, sie können nichts dafür.
• Man (vor allem Mitteleuropäer) sollte bei oben angeführten Temperaturen und sengender Sonne auf gar keinen Fall ohne Sonnenschutz durch Chania/Hania/Xania marschieren. Die merkwürdigsten Erkenntnisse können eintreffen.
• Das Problem des Abstandes zum Horizont ist mit dieser Berechnung eigentlich nur teilweise gelöst. Hier wird der Abstand des Horizontes zum Auge des Betrachters berechnet, und das Auge blickt bekanntlich ja gradeaus. Der Abstand des Horizontes zu den Füßen des Betrachters ist aber nach wie vor unbekannt. Unklar ist weiters, ob der Abstand der Füße zum Horizont bei den zu erwartenden Entfernungen als direkte Verbindungsgerade gesehen werden darf, oder der Erdkrümmung folgend als Kreisbogensegment berechnet werden muss.
• Interessant und signifikant werden diese theoretischen Unterschiede in der Abstandsmessung wohl erst, wenn mit Hilfe der Gentechnik Menschen entstehen, die über 10.000m Körpergröße und damit auch entsprechende Augenhöhe haben.
• Geklärt ist jetzt zwar, wie weit der Horizont entfernt ist. Aber wie man den Horizont vollständig entfernen kann, oder ob dies überhaupt möglich ist, ist noch unbeantwortet.

Aber all diese Probleme werden wohl erst gelöst werden, wenn ich das nächste Mal irgendwo in der Sonne vor mich hinsieche, und urplötzlich wieder den Drang verspüre, die Welt zu verbessern.

_________________________________________________________________________________________

Christoph in den wilden Bergen Kretas. Da war wohl auch ein Lindenberg / Underberg dabei und etwas Wodka oder Ouzo.

Im Kafenio sitzen, Zeit haben, mit Karten und Gedanken spielen.

Das könnt Ihr im Kafenio.eu bei Christoph. Geöffnet rund um die Uhr.

streamplus.de